受付時間
8:00-20:00(月~土)
8:00-19:00(日)
\メルマガ・LINE登録で全科目閲覧可能/
日本大学医学部2018年~2026年度までの医学部試験のYMS解答速報・過去問解答です。
\直前講習会からも大的中・的中連発!/
理科3科目に関しましてはメルマガ登録後の自動返信メール内URLをご確認ください。
※メールが届かない場合、迷惑メールに振り分けられている可能性がございます。
迷惑メールフォルダをご確認いただくか「noreply@kintoneapp.com」の受信設定をお願いいたします。
Ⅰ[小問集合](易)
2次方程式、2次不等式、複素数の計算、データの分析、数列からの基本問題の出題である。すべて落とさず得点したい。尚、(3)の後半は、分散の公式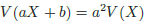 を活用したい。
を活用したい。
Ⅱ[三角関数](易)
tanに関する計算問題。(1)は半角公式を用いればよい。(2)は(1)の結果を用いて加法定理を計算すればよい。落とさず得点したい。
Ⅲ[指数・対数関数](易)
指数対数関数の計算問題である。これが一番易しく感じたかもしれない。落とさず得点したい。
Ⅳ[場合の数](標準)
番号の大小と組み合わせに関する典型問題である。(1)は異なる5数を選ぶ、(2)は4種類から4つ選ぶ重複組合せ、(3)は問題文に従って具体化すれば計算できる。計算は易しいため、落とさず得点したい。
Ⅴ[ベクトルと図形](標準)
台形とベクトルの典型問題である。問題に従って解いていけばよい。解答のように、幾何的に処理すると計算を減らすことができる。これも落とさず得点したい。
Ⅵ[数III 微積分](標準)
微積分に関する典型問題である。(1)は極値の条件を定式化すればよい。分数関数の極値に関する公式を知っていれば簡単に答えの数値を出すことができる。(2)の体積は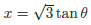 と置換する典型的な積分であるが計算ミスに注意したい。
と置換する典型的な積分であるが計算ミスに注意したい。
昨年度と比較して、難易度は同じかやや易しくなった。ベクトルの問題や、微積分の問題は難しくはないが差がつきそうである。
一次突破ボーダーは他の科目にもよるが90%程度か。
問題構成・出題形式ともに例年と同一であった。医学部A方式の廃止以来、分量・難易度ともに大幅に低減しており、引き続き高得点域での戦いとなることが予想される。医学部受験生ならば75〜80%以上は確保したいところ。
なお、二次での筆記試験では、従来のA方式と同じ形の長文問題が3本出題されるのが例年のスタイルである。一次通過者は、旧A方式の過去問演習をしておくことが有効であろう。
Ⅰ[小問集合](易)
積分計算からの出題であった。どれも平易な内容で落とせない。
Ⅱ[数Ⅲ微分法](やや易)
指数関数と対数関数の合成関数に関する出題であった。考え方は平易で計算がやや複雑であるが、時間を考えれば丁寧に計算していけばよいだけである。ここも落としたくない。
Ⅲ[極限](やや易)
無限級数からの出題であった。典型的な出題で,例年1 次試験(N1)で見られた出題が2次試験で出題された。特に難しい考え方なく、ここも落としたくない。
昨年度に比べると易化した。どれも典型的な出題で解法も決まっているものばかりであった。時間も考えれば正規合格ラインには1題も落とせないのではないだろうか。
マーク式の問い10問から成る長文が3本。大問構成・出題形式ともに例年通りである。PASSAGE1の5.と、PASSAGE2の12.にやや難しめの語彙/表現が含まれる以外は、選択肢の絞り込みも容易で、昨年度比でやや易化。時間的余裕もかなりあるので、本文と選択肢の一語一句を照合し、ケアレスミスのないよう抜かりなく解き進めたいところ。最終合格には80%以上の得点が望まれる。
3/4公開予定
理科3科目に関しましてはメルマガ登録後の自動返信メール内URLをご確認ください。
Ⅰ[小問集合](易)
集合、二次関数、対数、複素数平面、三角関数からの基本問題の出題である。全て落とさず得点したい。
Ⅱ[確率](易)
非常に基本的な問題である。落とさず得点したい。
Ⅲ[ベクトル](易)
垂心の位置ベクトルを求める基本問題である。落とさず得点したい。
Ⅳ[指数関数、整数](標準)
指数関数と格子点に関する問題。(2)までは得点したい。
Ⅴ[数列、極限](標準)
問題文をよく読み、図の設定を間違えないようにすることが重要な問題であった。計算自体は多くないため、落とさず得点したい。
Ⅵ[数Ⅲ微積分](標準)
回転体の体積に関する問題。𝓎軸回転をさせるときの立式をうまくできるかがポイントであった。
昨年度に比べて、難易度は上がった。格子点に関する問題や、図形を𝓎軸回転させる問題など、差が付きやすそうな出題が今年度は見られた。
1次突破ボーダーは他の科目にもよるが80%程度か。
問題構成・出題形式ともに昨年度と同一。極めて基本的な問いばかりなので、医学部受験生ならば80%以上は確保したいところ。
なお、二次での筆記試験では、従来のA方式に準ずる形の長文問題が3本出題されるのが例年のスタイルである。一次通過者は、旧A方式の過去問演習をしておくことが有効であろう。
Ⅰ[小問集合(積分法)](易)
基本的な積分計算からの出題であった。どれも基本的でここで絶対に落とすことはできない。
Ⅱ[関数、数Ⅲ積分法](やや易)
無理関数のグラフと直線に関する出題であった。特に難儀するところはないだろう。
Ⅲ[数Ⅲ微積分](標準)
積分方程式によって決まる関数に関する出題であった。複合的な内容であるがどれも入試基礎レベルの内容なのでしっかりと得点したい。
昨年度と比べて同程度であった。満点を目指したい内容であるが、2完半あたりが合格ラインか。
マーク式の問い10問から成る長文が3本。大問構成・出題形式ともに例年通りである。昨年度はPASSAGE3の語彙レベルが高くやや手を焼くものであったが、本年度は全体に読みやすく明らかな易化と言える。時間的余裕もかなりあるので、本文と選択肢の一語一句を照合し、ケアレスミスのないよう抜かりなく解き進めたいところ。最終合格には75%以上の得点が望まれる。
理科3科目に関しましてはメルマガ登録後の自動返信メール内URLをご確認ください。
Ⅰ[小問集合:三角比・極限・整数・図形と方程式・対数関数](易)
基礎的な問題であるので完答を狙いたい。
Ⅱ[複素数平面](易)
複素数平面における回転の問題であった。ミスなく計算したい。
Ⅲ[確率](易)
条件付き確率の問題であった。ここは完答したい。
Ⅳ[ベクトル](やや易)
空間ベクトルの問題であった。難しい問題ではないため、丁寧な計算を心がけ、完答を目指したい。
Ⅴ[三角関数・数Ⅲ微積分](標準)
媒介変数表示された関数に関する問題であった。(2)は見かけよりも難しくないため、ここまでは解けたい。
Ⅵ[数列](やや易)
漸化式の問題であった。誘導は丁寧であるため、しっかりと誘導に乗って解き切りたい。
昨年度と同程度の難易度か。基礎的な計算が多いため、ケアレスミスに注意したい。1次突破ボーダーは75~80%程度か。
問題構成・出題形式ともに例年とほぼ同一であった。唯一、大問Ⅵの会話文問題が今風のテキストメッセージからの出題となったが、問いそのものは平易であり特にうろたえるようなものではなかった。医学部A方式の廃止以来,分量・難易度ともに大幅に低減しており、引き続き高得点域での戦いとなることが予想される。医学部受験生ならば75〜80%以上は確保したいところ。
なお、二次での筆記試験では、従来のA方式に準ずる形の長文問題が3本出題されるのが例年のスタイルである。一次通過者は、旧A方式の過去問演習をしておくことが有効であろう。
Ⅰ[関数](やや易)直線と双曲線に関する出題であった。(2)は(1)を用いて解くのではなく、新たに座標を文字でおいて解くと計算が煩雑にならずに済むだろう。
Ⅱ[数Ⅱ微積分](やや易)円と放物線で囲まれた領域の面積を求める典型問題であった。特に難しいところはないので計算ミスのないようにしたい。
Ⅲ[三角関数](やや易)単位円の接線に関する出題であった。特に難しいところはないので計算ミスのないようにしたい。
昨年度と同程度の難易度であった。満点を目指したい内容であるが、1ミスあたりが合格最低ラインか。
マーク式の問い10問から成る長文が3本。大問構成・出題形式ともに例年通りである。時間的余裕もかなりあるので、本文と選択肢の一語一句を照合し、ケアレスミスのないよう抜かりなく解き進めたいところ。最終合格には75%以上の得点が望まれる。
理科3科目に関しましてはメルマガ登録後の自動返信メール内URLをご確認ください。
Ⅰ[小問集合](易)
三角比、ベクトル、2 次関数、図形と方程式、複素数からの基本問題の出題である。すべて落とさず得点したい。
Ⅱ[指数関数](易)
非常に基礎的な問題であるから落とさず得点したい。
Ⅲ[図形と方程式](易)
(2) の計算で行き詰まった人もいるかもしれないが基本レベルであるので落とさず得点したい。
Ⅳ[確率](易)
反復試行と条件付き確率の基本問題である。落とさず得点したい。
Ⅴ[数列](易)
階差数列、等比数列の基本問題である。落とさず得点したい。
Ⅵ[数Ⅲ微積分](標準)
無理関数と1次関数で囲まれる部分の面積、回転体の体積を求める問題である。体積の計算は少し計算が汚くなりやすいので差がついたと思われる。
全体的に去年より易しくなったと思われる。差がつきやすいのも体積の計算だけであとはどれも基本的な問題であるから計算ミスが致命傷になるので検算などをして気をつけよう。
1次突破ボーダーは他の科目にもよるが80~85%程度か。
問題構成・出題形式ともに昨年度と同一であった。医学部A方式の廃止以来,分量・難易度ともに大幅に低減しており、引き続き高得点域での戦いとなることが予想される。医学部受験生ならば75〜80%以上は確保したいところ。
なお、二次での筆記試験では、従来のA方式に準ずる形の長文問題が3本出題されるのが例年のスタイルである。一次通過者は、旧A方式の過去問演習をしておくことが有効であろう。
Ⅰ[小問集合](易)
基本的な定積分の出題であった。特に難しいところはなく、ここでは落とせない。
Ⅱ[数Ⅲ微分法](易)
不等式の証明の問題であった。誘導もあり、特に難しいところもなく、ここでは落とせない。
Ⅲ[数Ⅲ積分法](標準)
定積分で表された関数の最小値に関する問題であった。題材はありふれているが、計算にやや難儀する。ただ、時間も十分にあるので丁寧な計算を心がけたい。
昨年度に比べてやや易しくなった。方針はすぐに浮かぶのでいかに計算を間違わないかの勝負であるように思う。満点を目指したい。
大問構成・出題形式ともに例年通りであるが、付される注の量が減り、受験生にとっては単純に未知語が増えたであろうという点で、昨年度までに比べるとやや難化と言える。特にPASSAGE3は語彙レベルがかなり高く、文脈から推測しなければならない箇所が多かっただろう。とは言え時間的余裕のある試験には変わりないので、本文と選択肢の一語一句を照合し、ケアレスミスのないよう抜かりなく解き進めたいところ。
最終合格には70%以上の得点が望まれる。
理科3科目に関しましてはメルマガ登録後の自動返信メール内URLをご確認ください。
Ⅰ[小問集合](易)
1次不等式、データの分析、複素数と方程式、数列、ベクトルからの基本問題の出題である。すべて落とさず得点したい。
Ⅱ[数Ⅱ図形と方程式](易)
円と直線の位置関係についての問題である。中心と直線の距離を考えればよい。非常に基礎的な問題であるから落とさず得点したい。
Ⅲ[数A確率](易)
最短経路についての確率である。(1) は反復試行、(2) は右端を通る場合に注意して計算すればよい。基本レベルであるので落とさず得点したい。
Ⅳ[数Ⅱ三角関数](易)
三角関数の最大値・最小値についての問題。(1)はcos x についての2次関数になる。(2)は和積変換すればよいが、加法定理で展開してから合成してもよい。(3)合成すればよい。どれも落とさず得点したい。
Ⅴ[数Ⅲ面積](標準)
絶対値のついた積分に関する問題である。図を描くなどして、ミスのないように進めたい。
(3)でlogを1つに纏めることに苦労した受験生がいたと思われる。(2)までは落とさず得点したい。
Ⅵ[数Ⅲ式と曲線](標準)
極方程式についての問題である。(1)放物線の定義を思い出せたかで差がついただろう。
(2)は(1)を用いれば容易だが、経験により差がついたと思われる。
計算ミスが致命傷になるので検算などをして気をつけよう。
1次突破ボーダーは75~80%程度か。
問題構成・出題形式ともに昨年度と同一であった。医学部A方式の廃止以来、分量・難易度ともに大幅に低減しており、引き続き高得点域での戦いとなることが予想される。
医学部受験生ならば80%以上は確保したいところ。
なお、二次での筆記試験では、従来のA方式に準ずる形の長文問題が3本出題されるのが例年のスタイルである。一次通過者は、旧A方式の過去問演習をしておくことが有効であろう。
Ⅰ[数と式、集合と論証](やや易)
特に難しいところはないが、(2)の証明は経験の差が出るだろう。
Ⅱ[図形と方程式](標準)
平易な問題であるが、数値がやや汚いので、計算を工夫して行えるかが勝負を分け目で計算の仕方で差がつくだろう。
Ⅲ[数Ⅲ微積分](やや難)
考え方として難しいところはないが、計算がやや難儀である。まともに計算してもよいが、対称性や α>1 という条件などに注目するとある程度計算の目星もつき、だいぶやりやすくなるだろう。
昨年度に比べて難易度は上がっている。全てを解き切るのが厳しいであろうから得点できるところで計算ミスの内容に進めたい。
70%を目指したい。
大問構成・出題形式ともに例年通り。本年度N1期の二次は,使用される語彙の難度に比べて注の量が少ないなどやや難化傾向にあったが、N2期では例年通りの難易度に戻ったと言える。
特にPASSAGE1・2は非常に易しく、それだけ高得点域での戦いになるであろう。
最終合格には80%以上の得点が望まれる。
理科3科目に関しましてはメルマガ登録後の自動返信メール内URLをご確認ください。
Ⅰ[小問集合](易)
(1) 集合と論理、(2)2次方程式、(3)整数の性質、(4)図形と方程式、(5)対数関数からの出題であった。
どれも教科書基本レベルの問題であり、落とせない。
Ⅱ[複素数平面](易)
ド・モアブルの定理に関する出題であった。
教科書基本レベルの問題であり、落とせない。
Ⅲ[確率](易)
箱から球を取り出す確率に関する出題であった。
教科書基本レベルの問題であり、落とせない。
Ⅳ[空間図形](やや易)
空間の交点の位置ベクトルに関する出題であった。
教科書基本レベルの問題であるので、失点はできれば避けたい。
Ⅴ[極限](やや易)
無限等比数列に関する出題であった。
教科書基本レベルの問題であるので、失点はできれば避けたい。
Ⅵ[積分法](やや易)
定積分で表された関数に関する出題であった。![]() は整関数で、特に計算上も難しい箇所はない。失点はできれば避けたい。
は整関数で、特に計算上も難しい箇所はない。失点はできれば避けたい。
昨年よりやや易しくなった。平易な問題ばかりであったので、いかに素早く計算し計算ミスをしないかの勝負となっただろう。
一次突破ボーダーは80%程度か。
問題構成・出題形式ともに昨年度と同一であった。医学部A方式の廃止以来、分量・難易度ともに大幅に低減しており、引き続き高得点域での戦いとなることが予想される。
医学部受験生ならば75〜80%以上は確保したいところ。
なお、昨年度二次での筆記試験では、従来のA方式に準ずる形の長文が3本出題された。
一次通過者は、旧A方式の過去問演習をしておくことが有効であろう。
[1][小問集合](易)
(1)は3次方程式の解を求めるだけの問題である。
(2)は合同式を使うと計算が簡単になる。昨年と同様に教科書基礎レベルの問題であり、失点は避けたい。
[2][数Ⅲ微分法](やや易)
(1)(2)は基礎的な問題であり、どちらも落とせない。
(3)だけ計算量がやや多いため、ここを正確に解くことができるかがポイントであった。
[3][2次曲線](標準)
極方程式と双曲線に関する有名問題である。
(1)は計算量を減らすために図形的に考えるのが良いだろう。
(2)は双曲線を極方程式で表すことで証明は容易となる。
(3)は三平方の定理に気づき、(2)を利用して正解したい。極方程式に関する有名問題の経験の有無が差を生みそうである。
昨年度と同様、大問3つの構成であった。大問2と大問3は数Ⅲ微分法と2次曲線に関する問題であり、昨年度と似たような問題構成になっている。
応用力よりも堅実な計算がしっかりとできるか、各単元の基本的な知識が正確に身に付いているかを問う内容になっている。
正規合格ラインは60点満点中45~50点程度か。
日本大学医学部の入試では、昨年度から二次試験でも英語のマーク式試験が課されるようになった。とは言え、形式・難易度ともに過年度のA方式とほぼ同一であり、A方式の過去問に取り組むことで十分に対応可能である。
試験時間が旧A方式の75分から60分に短縮されたことで、大問数が4題から3題へと減少したが、時間的に余裕のある試験であることには変わりない。じっくり読む時間があると思われるので、本文と選択肢の一語一句を照合し、ケアレスミスのないよう抜かりなく解き進めたいところ。
最終合格には75%以上の得点が望まれる。
理科3科目に関しましてはメルマガ登録後の自動返信メール内URLをご確認ください。
Ⅰ[小問集合](易)
(1)2次方程式、(2)図形と方程式、(3)常用対数、(4)複素数と方程式、(5)図形と方程式からの出題であった。
どれも教科書例題レベルの問題であり,落とせない。
Ⅱ[確率](やや易)
じゃんけん、反復試行の確率の問題であった。典型的な問題であるので、確実に得点したい。
Ⅲ[三角関数](標準)
三角関数の最大値、最小値に関する典型問題。合成をして、丁寧に計算すればよい。
Ⅳ[数列、無限級数](やや易)
三角形の面積に関する、数列・無限級数の問題であった。(3)は初項がSではなくS1であることに注意。
教科書傍用問題集にあるような問題で、特に難しい箇所はない。失点はできるだけ避けたい。
Ⅴ[極限](やや易)
無限等比数列に関する出題であった。
教科書基本レベルの問題であるので、失点はできれば避けたい。
Ⅵ[積分法](やや易)
定積分で表された関数に関する出題であった。![]() は整関数で、特に計算上も難しい箇所はない。失点はできれば避けたい。
は整関数で、特に計算上も難しい箇所はない。失点はできれば避けたい。
昨年よりやや易しくなった。平易な問題ばかりであったので、いかに素早く計算し計算ミスをしないかの勝負となっただろう。
一次突破ボーダーは80%程度か。
問題構成・出題形式ともに例年通りであった。
医学部A方式の廃止以来、分量・難易度ともに大幅に低減しており、引き続き高得点域での戦いとなることが予想される。
医学部受験生ならば80%以上は確保したいところ。
なお、N1期二次での筆記試験では、昨年度に引き続き、従来のA方式に準ずる形の長文が3本出題された。
一次通過者は、旧A方式の過去問演習をしておくことが有効であろう。
[Ⅰ][数Ⅲ積分法](易) 基礎的な積分計算からの出題であった。この計算は1つも落としてはいけない。
[Ⅱ][数列、極限](やや易)
点列の極限からの出題であった。丁寧に計算を進めていけばよい。階差型の漸化式の計算には注意したい。
[Ⅲ][2次曲線](標準)
楕円と直線の共有点に関連する問題からの出題であった。計算量がやや多いが、難しい考え方を用いる問題ではない。
(3)以外は間違わずに解きたい。
昨年度のN2とはほぼ同程度の難易度、今年度のN1と比べると難易度は下がった。時間も十分にあることを考えると、正規合格には50点/60点は必要だろう。
理科3科目に関しましてはメルマガ登録後の自動返信メール内URLをご確認ください。
N方式ということもあってか、易しめの出題が多かった。ただし、問題量が多いので詰まった問題があったらすぐに飛ばして次に移るなど手早く解き進められたかが合否を分けることになるだろう。一次突破ラインは70% 程度か。
日本大学医学部の入試は本年度からA方式が廃止となり、N方式に統一となった。そのため、出題傾向も従来のN方式を踏襲する形となった。例年出題されていた発音・アクセント問題は出題されず、昨年度のN2期と同一の大問構成であった。昨年度までのA方式に比べて分量・難易度ともに大幅に低減し、高得点域での戦いとなることが予想される。医学部受験生ならば7.5~8割以上は確保したいところ。
なお、二次での筆記試験では、従来のA方式に準ずる形の医系長文が出題されることも想定されるため、今回高得点を収めた者も気を抜かず長文演習に努めて欲しい。
[ 1 ][小問集合](易)
教科書基礎レベルの問題で、ここでの失点は避けたいところ。
[ 2 ][数Ⅲ積分法](やや易)
逆関数に関する問題である。計算量も多くなく、ここでも失点は避けたい。
[ 3 ][数Ⅲ微分法](標準)
3つの大問の中で最も骨のある問題で、要領のよい計算が求められる。大問1、2を時間をかけずに終えて、大問3にしっかりと時間をかけて点数を稼ぎたい。
初の2次での学科試験ということもあり難易度についてわからないこともあったが、旧A方式の記述問題より易しめであった。高得点勝負になると考えられる。
正規合格ラインは60点満点中45~50点程度か。
日本大学医学部の入試では、本年度から二次試験でも英語のマーク式試験が課されるようになった。とは言え、形式・難易度ともに過年度のA方式とほぼ同一であり、一次試験通過者はA方式の過去問に取り組むことで十分に対応可能である。試験時間が昨年度までの75分から60分に短縮されたことで、大問数が4題から3題へと減少したが、時間的に余裕のある試験であることには変わりない。じっくり読む時間があると思われるので、本文と選択肢の一語一句を照合し、ケアレスミスのないよう抜かりなく解き進めたいところ。最終合格には80%以上の得点が望まれる。
1期と比較すると、全体として難易度は下がったように感じる。計算量も少なくなっており、高得点勝負になると考えられる。Ⅱ期の定員数も考えると、一次突破ラインは80%程度か。
大問構成・難易度・出題傾向ともにNⅠ期と同一であった。特に難解な問いはなく、いかにミスを防ぐかという高得点域での戦いとなることが予想される。医学部受験生ならば 8.5割以上は確保したいところ。
なお、N1期二次における筆記試験は、昨年度までのA方式とほぼ同一の形式(大問数は4題から3題に減少)であったことから、N2期の二次も同様の出題となることが予想される。
[ 1 ][整数の性質](易)
基本的な一次不定方程式からの出題であった。(2)はしらみつぶしに調べるしかないだろう。
[ 2 ][数Ⅲ微分法、数Ⅲ積分法](易)
基本的な微積分に関する出題であった。ここでの失点は避けたい問題ばかりで、素早く終わらせて大問3に時間を割いていくべきであろう。
[ 3 ][図形と方程式](標準)
3つの大問の中で最も骨のある問題で、要領のよい計算が求められる。大問1、2を時間をかけずに終えて、大問3にしっかりと時間をかけて点数を稼ぎたい。
N1期と同程度のレベルであった。高得点勝負になると考えられる。N1、N2期ともに大問2、3が関数絡みの出題で、特に大問3は図形的な考察を必要とする出題でもあった。正規合格ラインは60点満点中45~50点程度か。
理科3科目に関しましてはメルマガ登録後の自動返信メール内URLをご確認ください。
[ 1 ][小問集合]((1)易(2)やや易(3)易(4)易)
(1)は2次関数の最小値、(2)は組み合わせの確率および期待値、(3)は命題の審議、(4)は内接四角形の対角線の長さ、面積の問題である。どれも基本的な問題であるが、(2)の期待値の出題に戸惑った受験生も多かったかもしれない。
[ 2 ][小問集合]((1)易(2)やや易(3)やや易(4)やや易)
(1)は分数型の漸化式、(2)は半角公式利用の三角関数の最小値、(3)は法線ベクトル、(4)は無理関数の共有点に関する問題である。[ 1 ]と同じくどれも基本的な問題で、ここでの失点は痛い。
[ 3 ][微分法](標準)
(3)は一般角が求まらない典型問題である。受験生であれば何度も経験のある問題であり、取り組みやすかったのではないだろうか。完答を目指したい。
[ 4 ][数Ⅱ微分法](標準)
(3)で問題の意味を理解し、計算を工夫する必要がある。やや計算量が多いものの、問題としては平易なので、計算ミスなく進めたい。
[ 5 ][極限(数列)](やや難)
(3)の計算量もそこそこ多く、最後までたどり着くのは難しい。(2)(3)は漸化式は立っても論証不十分の答案も多いのではないだろうか。(2)まで答えを出せていれば十分だろう。
昨年度よりも計算量がやや増し、全体的に計算力を問う問題であったと言える。難易度としては大きく変わらなかった。目標は75%。
例年通り、10問ずつからなる長文の4題構成であった。昨年度までと異なり、語注は日本語ではなく英語での定義が与えられる形となり、英語の苦手な受験生にとっては読むのにやや余計な時間を要したかもしれない。しかし、試験時間75分は潤沢であり、大きな支障にはならなかったであろう。
設問も比較的素直なものが多い一方、上記講評で触れたものについては、審議に多大な時間を要する極めて微妙な問いであった。実際はそこまでの深読みを要求していないのかもしれないが、新しい「学力」の要素として思考力・判断力を要求する昨今の大学入試改革の潮流において、指導する立場にある我々予備校が徹底的に突き詰めて考えないわけにはいかなかった。
解答導出の明快さという点において、やや疑義の残った問いもあるのが事実であるが、客観的論理性を第一に考え上記をYMSの見解とする。
理科3科目に関しましてはメルマガ登録後の自動返信メール内URLをご確認ください。
①②(易)
小間集合。いずれも教科書レベルの内容であった。
③(やや易)
反復試行に関する確率の間題。(1)の誘導を利用し、(2)(3)が素早く解けたかが鍵を握る。
④(やや易)
(2)はグラフを描いて済ませるのではなく、記述であることも踏まえて解説のように![]() を持ち出し
を持ち出し![]() の符号をしっかりと調べていくのがよいだろう。
の符号をしっかりと調べていくのがよいだろう。
(3)は(2)の意味を考えて、与式の変形をしよう。
⑤(やや易)
計算だけであるが、計算ミスのないようにしたい。
例年通りいかにミスをせず失点を防ぐかが大事であった。高得点勝負になることは必至である。
一次突破ラインは80%超か。他の科目の出来が合否を分けるだろうが、数学での失敗は致命的である。
いずれの大問も大変取り組みやすく、場合によっては75分という試験時間を持て余してしまうほどであろう。それゆえかなりの高得点勝負となることが予想され、一つのケアレスミスが命取りとなりうる。設問はすべてにおいて該当箇所が明示されており、解答の根拠を明瞭に特定できる問いが大半を占めるので、本文の記述を丁寧に追いながら確実に解答していくことが肝要である。
「2023年度 日本大学N2期 直前講習会」から入試問題がズバリ大的中!!
「2023年度 日本大学N2期 直前講習会」から入試問題がズバリ大的中!!
これが実際の入試本番に活きる直前講習会
YMSの「日本大学医学部 直前講習会」から入試問題がズバリ大的中!!
これが実際の入試本番に活きる直前講習会
\毎年YMS模試から大的中・的中連発!模試受験者は有利に!/
YMSは受験技術を教えるだけでなく
「いい医者」を育てることを
目標にしています。